SSD实现

Part0-整体网络模型

  • VGG Backbone
  • Extra Layers
  • Multi-box Layers

Part1-VGG Backbone

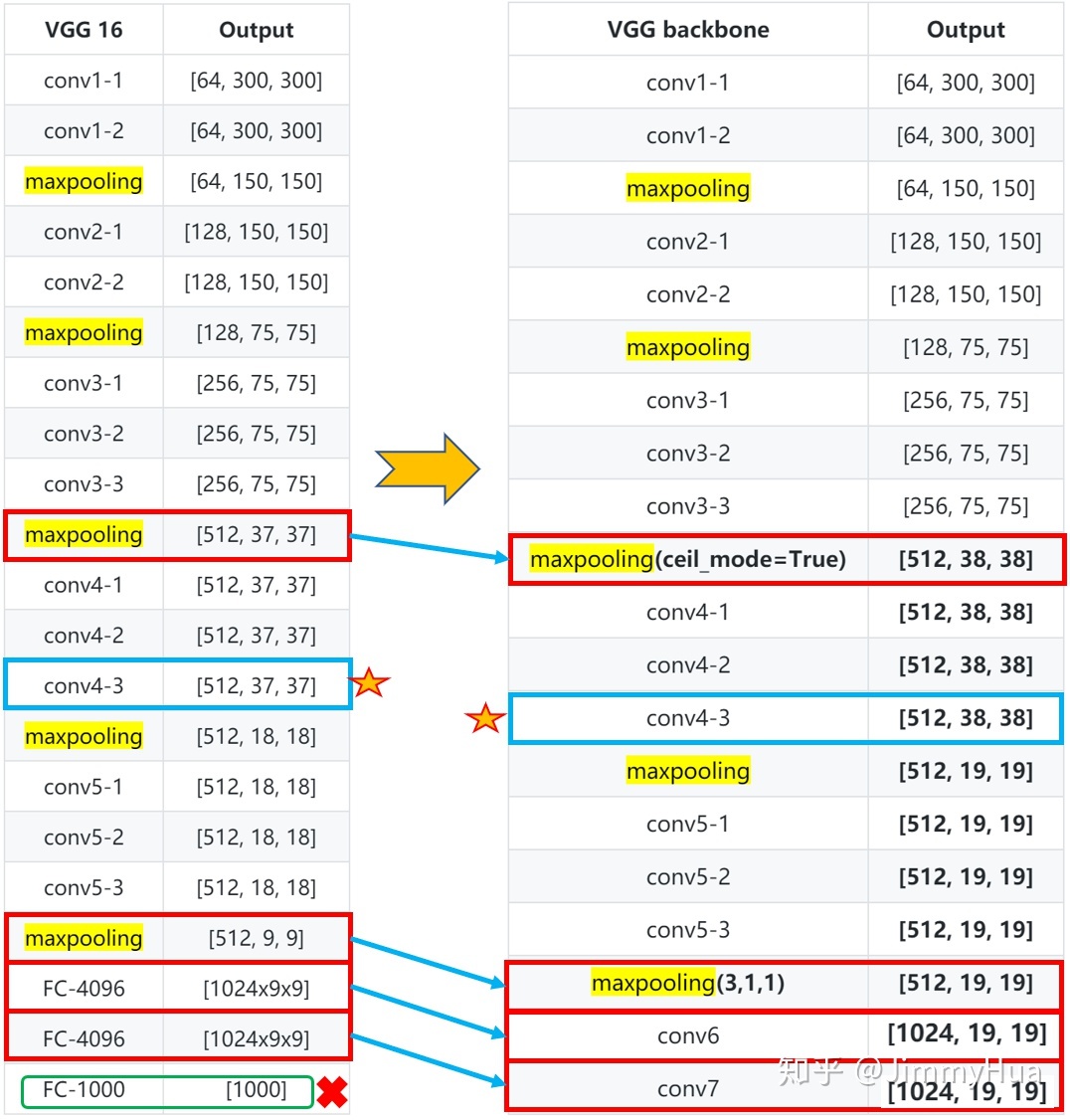
v2-6e73f4f987013d933744bf70045b3aa8_r.jpg

SSD首先使用了vgg16作为base网络，但做了一些小修改，即用卷积层替代vgg16原本的FC6,FC7两个全连接层。改动主要如下：

  • 为了能够与在骨干网络之后增加特征提取层，将全连接层fc6和fc7转换为卷积层conv6和conv7，并对fc6和fc7的参数进行二次采样，并移除了fc8层；
  • 将池化层pool5从2×2大小，步长为2更改为3×3大小，步长为1，并使用atrous算法来填充“漏洞”；
  • 由于SSD网络结构移除了VGG16的全连接层，因此防止过拟合的dropout层也被移除；
  • 由于conv4_3与其他特征层相比具有不同的特征比例，因此使用L2归一化将特征图中每个位置的特征比例进行缩放，并在反向传播过程中学习该比例。

先写配置文件：（SSD分为300和512两个版本，这里以300为例）

1
2
3
4
5
vgg_base = {
    '300': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 'C', 512, 512, 512, 'M',
            512, 512, 512],
    '512': [],
}

然后按照配置填写vgg网络layer：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 该部分为vgg源码
def vgg(batch_norm=False):
    cfg = vgg_base['300']
    in_channels = 3
    layers = []
    for v in cfg:
        if v == 'M':
            layers += [nn.MaxPool2d(kernel_size=2, stride=2)]
        elif v == 'C':
            layers += [nn.MaxPool2d(kernel_size=2, stride=2, ceil_mode=True)]
        else:
            conv2d = nn.Conv2d(in_channels, v, kernel_size=3, padding=1)
            if batch_norm:
                layers += [conv2d, nn.BatchNorm2d(v), nn.ReLU(inplace=True)]
            else:
                layers += [conv2d, nn.ReLU(inplace=True)]
            in_channels = v
    pool5 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)

    # 至此实现了vgg16原本的前5个block，后面为SSD自己的修改
    conv6 = nn.Conv2d(512, 1024, kernel_size=3, padding=6, dilation=6)
    conv7 = nn.Conv2d(1024, 1024, kernel_size=1)
    layers += [pool5, conv6,
               nn.ReLU(inplace=True), conv7, nn.ReLU(inplace=True)]
    return layers

用个小测试数据测试一下：

1
2
3
4
5
6
7
if __name__ == '__main__':
    x = torch.randn(1, 3, 300, 300)
    layers = vgg()
    for net in layers:
        x = net(x)
    print(x.shape)
# 返回(1, 1024, 19, 19)

Part2-Extra Layers

v2-08e3a953a8d29f6d72e6416fa609c804_r.jpg

  • Extra网络层的设计主要是为了后续多尺度提取
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
net_extras = {
    '300': [256, 'S', 512, 128, 'S', 256, 128, 256, 128, 256],
    '512': [],
}
# 返回一个extra的layer列表
def extra_net():
    # Extra layers added to VGG for feature scaling
    layers = []
    cfg = net_extras['300']
    in_channels = 1024
    flag = False
    for k, v in enumerate(cfg):
        if in_channels != 'S':
            if v == 'S':
                layers += [nn.Conv2d(in_channels, cfg[k + 1],
                                     kernel_size=(1, 3)[flag], stride=2, padding=1)]
            else:
                layers += [nn.Conv2d(in_channels, v, kernel_size=(1, 3)[flag])]
            flag = not flag
        in_channels = v
    return layers
1
2
3
if __name__ == '__main__':
    layer = extra_net()
    print(nn.Sequential(*layer))

Part3-Multi-box Layers

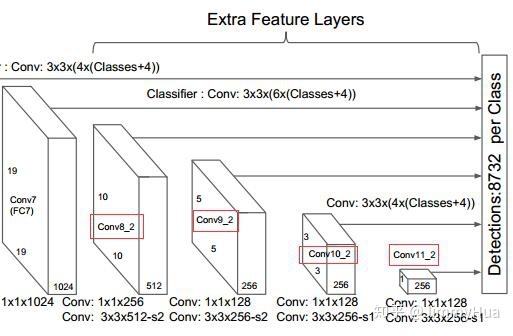
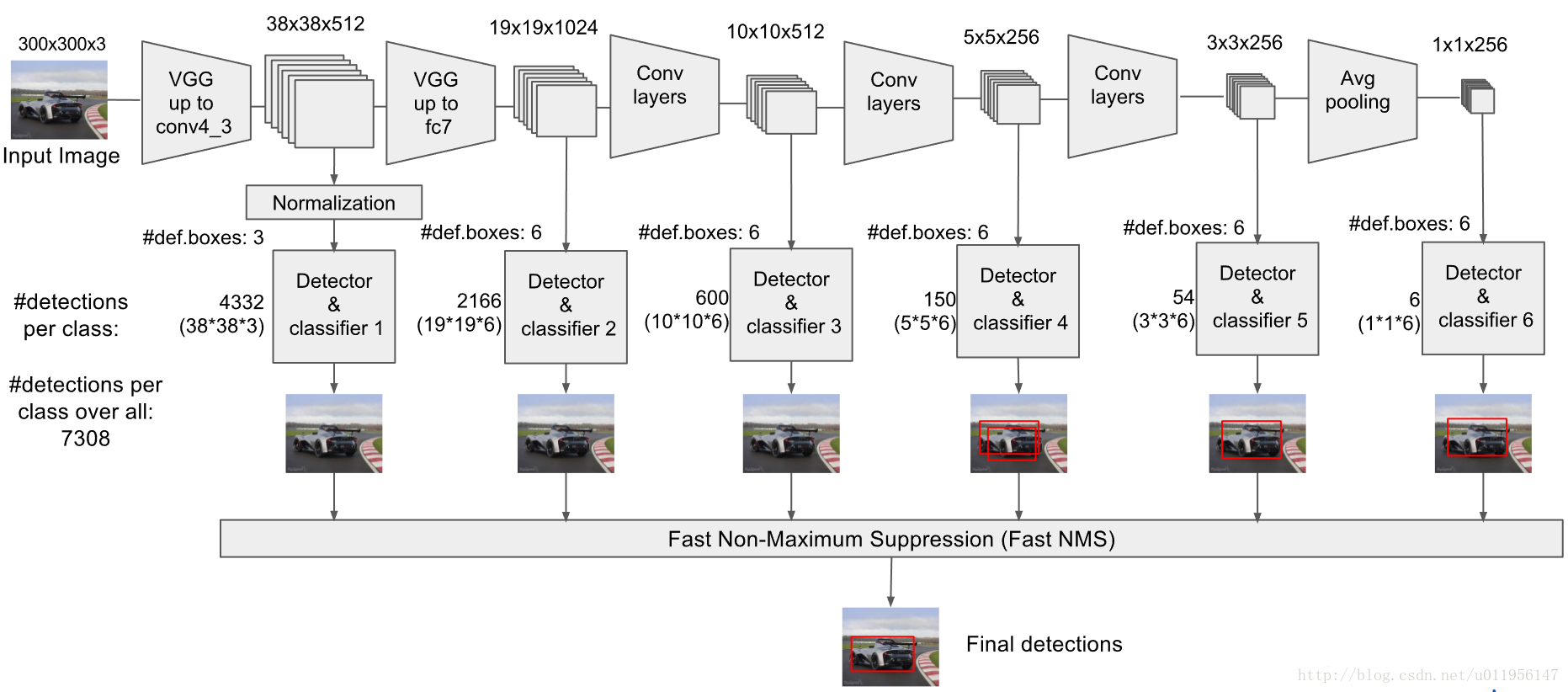
20170611145131140.png

由图片中我们可以看到，从conv4_3开始，SSD一共提取了6个特征图。其大小分别为 (38,38),(19,19),(10,10),(5,5),(3,3),(1,1)，但是每个特征图上设置的先验框数量不同。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
multi_box_cfg = [4, 6, 6, 6, 4, 4]
# 用于多尺度分析的multi_box
def multi_box_net():
    """
    Return:
        vgg, extra_layers
        loc_layers: 多尺度分支的回归网络
        conf_layers: 多尺度分支的分类网络
    """
    vgg_layers = vgg_net()
    extra_layers = extra_net()
    loc_layers = []
    conf_layers = []
    vgg_source = [24, -2]
    num_classes = 21
    cfg = multi_box_cfg
    for k, v in enumerate(vgg_source):
        loc_layers += [nn.Conv2d(vgg_layers[v].out_channels,
                                 cfg[k] * 4, kernel_size=3, padding=1)]
        conf_layers += [nn.Conv2d(vgg_layers[v].out_channels,
                                  cfg[k] * num_classes, kernel_size=3, padding=1)]
    for k, v in enumerate(extra_layers[1::2], 2):
        loc_layers += [nn.Conv2d(v.out_channels, cfg[k]
                                 * 4, kernel_size=3, padding=1)]
        conf_layers += [nn.Conv2d(v.out_channels, cfg[k]
                                  * num_classes, kernel_size=3, padding=1)]
    return vgg_layers, extra_layers, (loc_layers, conf_layers)
1
2
3
4
5
if __name__ == '__main__':
    vgg_layers, extra_layers, (loc, conf) = multi_box_net()
    print(nn.Sequential(*loc))
    print('---------------------------')
    print(nn.Sequential(*conf))

Part4-SSD类

在写SSD类之前，我们先要了解几个概念。

Prior Box

  • SSD从Conv4_3开始，一共提取了6个特征图，其大小分别为 (38,38),(19,19),(10,10),(5,5),(3,3),(1,1)，但是每个特征图上设置的先验框数量不同。

  • 尺度$s_k$表示先验框大小相对于图片的比例;

  • 先验框的设置，包括尺度（或者说大小）和长宽比两个方面。对于先验框的尺度，其遵守一个线性递增规则：随着特征图大小降低，先验框尺度线性增加：

  • 对于第一个特征图，尺度取0.1，剩余5个在0.2($s_{min}$)-0.9($s_{max}$)间均匀取值。

由于这样算出的先验框尺寸可能会产生小数，而对于一个300*300的原图像，没有小数的像素，因此，我们将尺度先×100再均分，由此得到的序列为{10，20，37，54，71，88}，然后再将其除以100，乘以300(换算成原图中的像素)：则先验框尺寸为{30，60，111，162，213，264}

  • 先验框的长宽比$a_r$一般设置为:{1, 2, 3, 1/2, 1/3}
  • 为保证同样的尺寸下，不同长宽比的先验框面积不变，有:$wh=s_ks_k$，同时满足长宽比$w/h=a_r$，由此有：$w=s_k\sqrt{a_r}$，$h=\frac{s_k}{\sqrt{a_r}}$
  • 在以上的基础上，还增加了一个正方形先验框，尺度为$\sqrt{s_k{s_{k+1}}}$，由于最后一个没有$s_{k+1}$，我们设置一个虚拟的$s_{k+1}=315$
  • 因此，每个特征图一共有 6 个先验框 {1,2,3,1/2,1/3,1′} ，但是在实现时，Conv4_3，Conv10_2和Conv11_2层仅使用4个先验框，它们不使用长宽比为 3,1/3 的先验框

由此我们可以写出prior_box类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class PriorBox(object):
    def __init__(self, cfg):
        super(PriorBox, self).__init__()
        self.image_size = cfg['min_dim']
        # number of priors for feature map location (either 4 or 6)
        self.num_priors = len(cfg['aspect_ratios'])
        self.variance = cfg['variance'] or [0.1]
        self.feature_maps = cfg['feature_maps']
        self.min_sizes = cfg['min_sizes']
        self.max_sizes = cfg['max_sizes']
        self.steps = cfg['steps']
        self.aspect_ratios = cfg['aspect_ratios']
        self.clip = cfg['clip']
        self.version = cfg['name']
        for v in self.variance:
            if v <= 0:
                raise ValueError('Variances must be greater than 0')

    def forward(self):
        mean = []
        # 开始遍历特征图 k为下标 f为边长
        for k, f in enumerate(self.feature_maps):
            # 对特征图的每个格子进行操作
            for i, j in product(range(f), repeat=2):
                # steps[k]表示第k个特征图中单个格子的边长大小
                f_k = self.image_size / self.steps[k]
                # 由此cx，cy即为该中心点相对整体的位置
                cx = (j + 0.5) / f
                cy = (i + 0.5) / f

                # s_k为该特征图对应的尺度
                s_k = self.min_sizes[k] / self.image_size
                # 加入长宽比为1的先验框
                mean += [cx, cy, s_k, s_k]

                # 求出根号s_k*s_k+1,并加入长宽比为1‘的先验框（与上个相比尺度不同）
                s_k_prime = sqrt(s_k * (self.max_sizes[k]/self.image_size))
                mean += [cx, cy, s_k_prime, s_k_prime]

                # 加入剩下四种先验框
                for ar in self.aspect_ratios[k]:
                    mean += [cx, cy, s_k * sqrt(ar), s_k / sqrt(ar)]
                    mean += [cx, cy, s_k / sqrt(ar), s_k * sqrt(ar)]

        # back to torch land
        output = torch.Tensor(mean).view(-1, 4)
        if self.clip:
            output.clamp_(max=1, min=0)
        return output

SSD类如下（不包括test部分）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class SSD(nn.Module):
    def __init__(self, phase, num_classes=9):
        super(SSD, self).__init__()
        self.phase = phase
        self.num_classes = num_classes

        # 初始化先验框
        self.prior_box = PriorBox(HiXray_cfg)
        self.priors = self.prior_box.forward()

        self.vgg = nn.ModuleList(vgg_net())
        self.L2Norm = L2Norm(512, 20)
        self.extra = nn.ModuleList(extra_net())

        head = multi_box_net()
        self.loc = nn.ModuleList(head[0])
        self.conv = nn.ModuleList(head[1])
        
        //	下面这部分到Detect再说
        if phase == 'test':
            self.softmax = nn.Softmax()
            self.detect = Detect()

Part5-损失函数

SSD的损失函数包括两部分的加权：

  • 位置损失函数 $L_loc$
  • 置信度损失函数 $L_conf$

我们首先了解一下$L_1\ Loss$,$L_2\ Loss$,和$Smooth\ L_1\ Loss$

L1 Loss

公式为：$L_1=\sum_{i=1}^n{|y_i-f(x_i)|}$

设x为预测值与真实值之间的差异，则$L_1=|x|$

特点：

  • L1 Loss在零点处不平滑
  • L1损失函数对差异x的导数为常数，因此如果学习率不变，损失函数会在稳定值附近波动，很难收敛

L2 Loss

公式为：$L_2=\sum_{i=1}^n{(y_i-f(x_i))^2}$

设x为预测值与真实值之间的差异，则$L_2=x^2$

特点：

  • L2 loss由于是平方增长，因此学习快。
  • L2损失函数对x的导数为2x，当x很大的时候，导数也很大，使 L2 损失在总loss 中占据主导位置，进而导致，训练初期不稳定。

Smooth L1 Loss

在Fast RCNN论文中被首次提出

公式：设x为预测值与真实值之间的差异：

$$Smooth_{L_1}=\begin{cases}0.5x^2 & |x| < 1\|x|-0.5 & |x|>=1 \end{cases}$$

特点：

  • 相比L1 Loss，Smooth L1 Loss解决了零点不平滑的问题
  • 相比L2 Loss，Smooth L1 Loss在x较大的时候变化比较缓慢